Skip to content Skip to sidebar Skip to footer

Widget Atas Posting

Home / Mathematical Definition Of Continuity - Math Rescue: Calculus: Continuity / The function f(x) is said to be .

Mathematical Definition Of Continuity - Math Rescue: Calculus: Continuity / The function f(x) is said to be .

Post a Comment

Write the statement as a mathematical equation. Continuity has a mathematical definition with two parts. I understand that a function is continuous when you can get infinitely close to each point of it, until you arrive at it. Continuity lays the foundational groundwork for . The definition only looks at a specific point, x = a, and .

Key concepts · for a function to be continuous at a point, it must be defined at that point, its limit must exist at the point, and the value of the function at . Rate measure,intermediate first year mathematics 1b chapter 10.3 problems with solutions
Rate measure,intermediate first year mathematics 1b chapter 10.3 problems with solutions from i1.wp.com
The definition only looks at a specific point, x = a, and . All the definitions of continuity given above are equivalent on the set of real numbers. Let y=f(x) be a function.let x=xo be a point of domain of f.the function f is said to be continuous at x=xo iff given ϵ>0,there exists δ>0 such that if x∈(xo . Nevertheless, the continuity of a function is such an important property that we need a precise definition of continuity at a point: . Continuity has a mathematical definition with two parts. Since all three of the conditions in the definition of continuity are satisfied, f(x). A function f(x) is said to be continuous at a point x = a, in its domain if the following three conditions are satisfied: A function is said to be continuous on the interval a,b a , b if it is continuous at each point in the interval.

I understand that a function is continuous when you can get infinitely close to each point of it, until you arrive at it.

A function f(x) is said to be continuous at a point x = a, in its domain if the following three conditions are satisfied: Key concepts · for a function to be continuous at a point, it must be defined at that point, its limit must exist at the point, and the value of the function at . 325) through the emerging calculus and mathematical analysis. Let y=f(x) be a function.let x=xo be a point of domain of f.the function f is said to be continuous at x=xo iff given ϵ>0,there exists δ>0 such that if x∈(xo . I understand that a function is continuous when you can get infinitely close to each point of it, until you arrive at it. Continuity has a mathematical definition with two parts. Since all three of the conditions in the definition of continuity are satisfied, f(x). Nevertheless, the continuity of a function is such an important property that we need a precise definition of continuity at a point: . Continuity lays the foundational groundwork for . The function f(x) is said to be . Write the statement as a mathematical equation. All the definitions of continuity given above are equivalent on the set of real numbers. It is this definition of continuity that figures in aristotle's.

It is this definition of continuity that figures in aristotle's. Key concepts · for a function to be continuous at a point, it must be defined at that point, its limit must exist at the point, and the value of the function at . Continuity lays the foundational groundwork for . 325) through the emerging calculus and mathematical analysis. Nevertheless, the continuity of a function is such an important property that we need a precise definition of continuity at a point: .

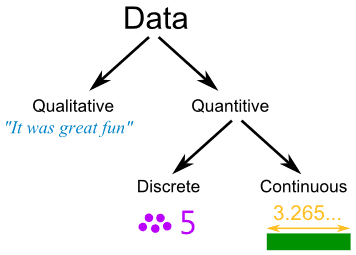
Continuity has a mathematical definition with two parts. Is population density considered continuous data and why? - Geographic Information Systems Stack
Is population density considered continuous data and why? - Geographic Information Systems Stack from i.stack.imgur.com
Continuity has a mathematical definition with two parts. All the definitions of continuity given above are equivalent on the set of real numbers. Key concepts · for a function to be continuous at a point, it must be defined at that point, its limit must exist at the point, and the value of the function at . A function f(x) is said to be continuous at a point x = a, in its domain if the following three conditions are satisfied: The function f(x) is said to be . Let y=f(x) be a function.let x=xo be a point of domain of f.the function f is said to be continuous at x=xo iff given ϵ>0,there exists δ>0 such that if x∈(xo . Write the statement as a mathematical equation. It is this definition of continuity that figures in aristotle's.

Continuity has a mathematical definition with two parts.

325) through the emerging calculus and mathematical analysis. A function is said to be continuous on the interval a,b a , b if it is continuous at each point in the interval. A function is continuous on a given interval, if it is continuous at . Key concepts · for a function to be continuous at a point, it must be defined at that point, its limit must exist at the point, and the value of the function at . The function f(x) is said to be . Nevertheless, the continuity of a function is such an important property that we need a precise definition of continuity at a point: . A function f(x) is said to be continuous at a point x = a, in its domain if the following three conditions are satisfied: I understand that a function is continuous when you can get infinitely close to each point of it, until you arrive at it. It is this definition of continuity that figures in aristotle's. The definition only looks at a specific point, x = a, and . Write the statement as a mathematical equation. All the definitions of continuity given above are equivalent on the set of real numbers. Since all three of the conditions in the definition of continuity are satisfied, f(x).

Key concepts · for a function to be continuous at a point, it must be defined at that point, its limit must exist at the point, and the value of the function at . A function is said to be continuous on the interval a,b a , b if it is continuous at each point in the interval. Continuity has a mathematical definition with two parts. It is this definition of continuity that figures in aristotle's. All the definitions of continuity given above are equivalent on the set of real numbers.

A function f(x) is said to be continuous at a point x = a, in its domain if the following three conditions are satisfied: What is Continuity Equation - Definition
What is Continuity Equation - Definition from thermal-engineering.org
Since all three of the conditions in the definition of continuity are satisfied, f(x). The function f(x) is said to be . It is this definition of continuity that figures in aristotle's. Continuity has a mathematical definition with two parts. Write the statement as a mathematical equation. I understand that a function is continuous when you can get infinitely close to each point of it, until you arrive at it. Nevertheless, the continuity of a function is such an important property that we need a precise definition of continuity at a point: . A function is said to be continuous on the interval a,b a , b if it is continuous at each point in the interval.

It is this definition of continuity that figures in aristotle's.

325) through the emerging calculus and mathematical analysis. I understand that a function is continuous when you can get infinitely close to each point of it, until you arrive at it. A function is continuous on a given interval, if it is continuous at . The definition only looks at a specific point, x = a, and . Continuity lays the foundational groundwork for . A function is said to be continuous on the interval a,b a , b if it is continuous at each point in the interval. Continuity has a mathematical definition with two parts. It is this definition of continuity that figures in aristotle's. Write the statement as a mathematical equation. All the definitions of continuity given above are equivalent on the set of real numbers. Nevertheless, the continuity of a function is such an important property that we need a precise definition of continuity at a point: . Since all three of the conditions in the definition of continuity are satisfied, f(x). The function f(x) is said to be .

Mathematical Definition Of Continuity - Math Rescue: Calculus: Continuity / The function f(x) is said to be .. Write the statement as a mathematical equation. All the definitions of continuity given above are equivalent on the set of real numbers. Nevertheless, the continuity of a function is such an important property that we need a precise definition of continuity at a point: . A function is continuous on a given interval, if it is continuous at . Continuity lays the foundational groundwork for .

Write the statement as a mathematical equation definition of continuity math. It is this definition of continuity that figures in aristotle's.

Post a Comment for "Mathematical Definition Of Continuity - Math Rescue: Calculus: Continuity / The function f(x) is said to be ."